深度学习第四节（激活函数和损失函数）

​ 激活函数和损失函数时深度学习模型中的重要组成部分，激活函数和损失函数的选择在很大程度上决定了深度神经网络的的性能和精度

1.常用激活函数

​ 使用激活函数可以实现网络的高度非线性

1.1sigmod激活函数

​ 使用范围最广，取值范围为[0,1],它可以讲一个实数映射到[0,1]的区间，可以将其用于二分类问题。函数形状为s型，称为s型生长曲线。

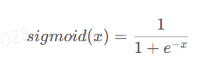
image-20250913171015309

1
2
def sigmod(x):
	return 1/(1+np.exp(-x))
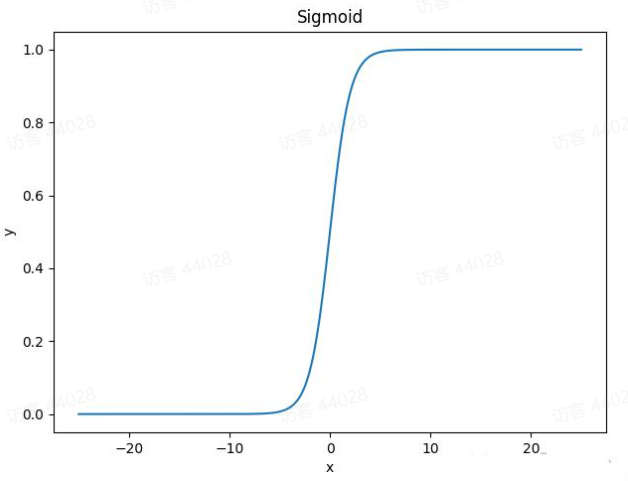
image-20250913171135218

优点：平滑易于求导

缺点：反向传播求导涉及除法，因此计算量大；反向传播时，很容易就会出现梯度消失的情况，限制了深层网络的训练。

1.2Tanh激活函数

Tanh是双曲函数的一种，是sigmod函数的改进，以0为中心，取值范围为[-1,1]

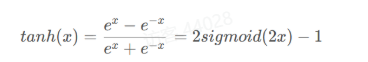
image-20250913171646616

1
2
def tanh(x):
	return (np.exp(x) - np.exp(-x))/(np.exp(x))+np.exp(-x))
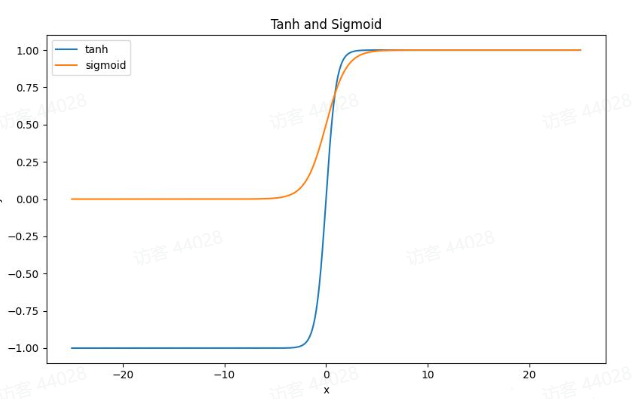
image-20250913171823784

优点：tanh函数是sigmod函数的改进，收敛速度快，不易出现loss值晃动

缺点：无法解决梯度弥散的问题，函数的计算量同样是指数级别的，计算复杂

1.3ReLU激活函数

修正线性单元激活函数的sigmod和tanh的完美替代激活函数，是深度学习领域最重要的突破技术之一

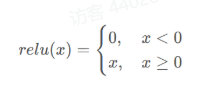
image-20250913172033765

1
2
def relu(x):
	return np.where(x>0,x,0)
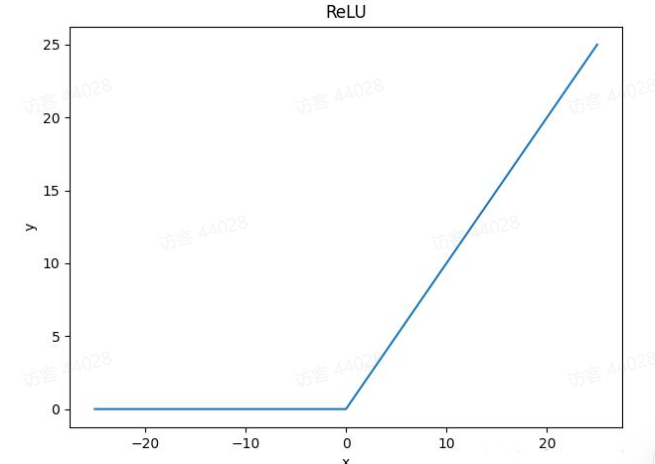
image-20250913172156231

​ 因为ReLU函数的大于等于0的线性分量具有固定导数，而对另一个线性分量导数为0.因此ReLU函数训练模型要快得多。

优点：不存在梯度消失问题，计算成本低，收敛速度比sigmod和tanh快很多

缺点：当梯度值过大，权重更新后为负数，在ReLU函数中导数恒为0，导致后面的梯度不更行，称为dying ReLU问题

1.4线性激活函数

线性激活的输出是输入本身，按照原样输出输入值，仅用于解决回归问题的神经网络模型的输出层，注意不能在隐藏层中使用线性激活函数

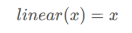
image-20250913172520937

1
2
def linear(x):
	return x

1.5softmax激活函数

通常softmax函数在神经网络输出最终结果前使用，通常使用softmax是为了确定输入在给定场景中属于n个可能的类别之一的概率。

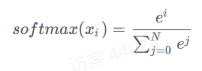
image-20250913172810007

1
2
def softmax(x):
	return np.exp(x)/np.sum(np.exp(x))

2.常用损失函数

​ 利用损失函数计算损失值，模型就可以通过反向传播去更新各个参数，通过降低真实值和预测值之间的损失，使得模型计算得到预测值趋近与真实值。损失函数的选择取决于问题的类型和所需的输出结果。

2.1均方误差（MSE）

​ 预测值p和实际值y之间的均方误差，当神经网络需要预测连续值时，通常使用均方误差。

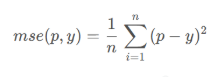
image-20250913174209543

1
2
def mse(p,y):
	return np.mean(np.square(p-y))

2.2平均绝对误差（MAE）

​ 平均绝对误差通过对所有数据点上的实际值和预测值之间的绝对差值取平均值，从而确保正误差和负误差不会相互抵消。也是用于连续变量值的预测

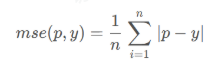
image-20250913174518961

1
2
def mae(p,y):
	return np.mean(np.abs(p-y))

2.3分类交叉熵

​ 交叉熵是对两种不同分布（实际分布和预测分布）之间差异的度量。广泛用于离散值输出数据。当预测值与实际值差距过大，分类交叉熵具有较高的值，而当与实际值接近时，分类交叉熵损失具有较低的值。

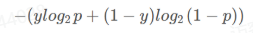
image-20250913174732579

1
2
def categorical_cross_entropy(p,y):
	return -np.sum(y*np.log2(p)+(1-y)*np.log2(1-p))

3.定义自定义损失函数

​ 在实际场景中，有时需要针对需要解决的问题子定义损失函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
x = [[1,2],[3,4],[5,6],[7,8]]
y = [[3],[7],[11],[15]]

import torch 
import torch.nn as nn
from torch.utils.data import Dataset,DataLoader

X = torch.tensor(x).float()
Y = torch.tensor(y).float()
device = 'cuda' if torch.cuda.is_available() else 'cpu'
X = X.to(device)
Y = Y.to(device)

class MyDataset(Dataset):
	def __init__(self,x,y):
		self.x = x.clone().detach()
		self.y = y.clone().detach()
	def __len__(self):
		return len(self.x)
	def __getitem__(self,ix):
		return self.x[ix],self.y[ix]

ds = MyDataset(X,Y)
dl = DataLoader(ds,batch_size=2,shuffle=True)

class MyNeuralNet(nn.Module):
	def __init__(self):
		super().__init__()
		self.input_to_hidden_layer = nn.Linear(2,8)
		self.hidden_layer_activation = nn.ReLU()
		self.hidden_to_output_layer = nn.Linear(8,1)
	def forward(self,x):
		x = self.input_to_hidden_layer(x)
		x = self.hidden_layer_activation(x)
		x = self.hidden_to_output_layer(x)
		return x
mynet = MyNeuralNet().to(device)

1.定义自定义损失函数，将两个张量对象作为输入，计算他们的差的平方，并返回两者平方差的平均值。

1
2
3
4
5
6
def my_mean_squared_error(_y,y):
	loss = (_y-y)**2
	loss = loss.mean()
	return loss
print(my_mean_squared_error(mynet(X),Y))
#tensor(81.3849, device='cuda:0', grad_fn=<MeanBackward0>)

2.使用相同的输入和输出组合，调用内置的MSELoss函数

1
2
3
4
loss_func = nn.MSELoss()
loss_value = loss_func(mynet(X),Y)
print(loss_value)
#tensor(81.3849, device='cuda:0', grad_fn=<MseLossBackward0>)