深度学习第三节(使用Pytorch构建神经网络) 神经网络通常包括输入层、隐藏层、输出层、激活函数、损失函数和学习率等基本组件。本节介绍在简单数据集上使用pytorch构建神经网络,利用张量对象操作和梯度值计算更新网络权重。
1.pytroch构建神经网络 解决两个数字的相加问题
1.初始化数据集
1 2 3 import torch x = [[1,2],[3,4],[5,6],[7,8]] y = [[3],[7],[5],[11]]
2.将输入列表转换为张量对象,并转换为浮点对象,此外将输入X和输出Y数据点注册到device中
1 2 3 4 5 6 X = torch.tensor(x).float() Y = torch.tensor(y).float() device = 'cuda' if torch.cuda.is_available else 'cpu' X = X.to(device) Y = Y.to(device)
3.定义神经网络架构,导入torch.nn模块用于构建神经网络模型,创建MyNeuralNet,继承自nn.Module,nn.Module是所有神经网络模块的基类
1 2 3 4 5 6 7 8 9 10 from torch import nn class MyNeuralNet(nn.Module): def __init__(self): super().__init__() #定义神经网络中的网络层 self.input_to_hidden_layer = nn.Linear(2,8) #全连接层以2个值作为输入并输出8个值,且包含与之关联的偏置参数 self.hidden_layer_activation = nn.ReLU() self.hidden_to_output_layer = nn.Linear(8,1)
注释:使用__init__方法初始化神经网络的所有组件,调用super().__init__()可以利用nn.Module编写的所有预构建函数,初始化的组件将用于MyNeuraNet类中的不同方法。全连接层(self.input_to_hidden_layer),使用ReLU激活函数的隐藏层(self.hidden_layer_activation),最后也是一个全连接层(self.hidden_to_output_layer)
4.将初始化的神经网络组件连接在一起,并定义网络的前向传播方法forward:
1 2 3 4 5 def forward(self,x): x = self.input_to_hidden_layer(x) x = self.hidden_layer_activation(x) x = self.hidden_to_output_layer(x) return x
注意:必须使用forward作为前向传播的函数名,因为Pytorch保留此函数作为执行前向传播的方法,使用其他名称都会引发错误。
5.执行以下代码访问每个深井网络组件的初始权重
1 2 #创建MyNeuralNet对象的实例并将其注册到device mynet = MyNeuralNet().to(device)
1 2 3 4 5 6 7 8 9 10 11 12 print(mynet.input_to_hidden_layer.weight) #类似代码可以访问每一层的权重和偏置 #Parameter containing: #tensor([[-0.4344, 0.3873], [ 0.3148, 0.6663], [ 0.5689, -0.5287], [-0.6481, 0.1600], [ 0.1827, -0.1818], [-0.6489, 0.0926], [ 0.1215, 0.4913], [ 0.2923, -0.6248]], device='cuda:0', requires_grad=True) #每次执行时输出的值并不相同,因为神经网络每次都使用随机值进行初始化,如果希望在执行相同代码时保持相同输出,需要在创建类对象的实例之前使用Torch中的manual_seed方法指定随机种子,torch.manual_seed(0)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 mynet.parameters() #可以获得神经网络的所有参数,会返回一个生成器,通过生成器循环获取参数 for param in mynet.parameters(): print(param) #代码结果如下: Parameter containing: tensor([[-0.1700, 0.1255], [-0.6442, -0.0863], [ 0.0079, -0.1979], [-0.3271, -0.3621], [-0.5230, 0.5031], [-0.6461, -0.5630], [ 0.3262, -0.0498], [ 0.3311, 0.3402]], device='cuda:0', requires_grad=True) Parameter containing: tensor([ 0.0449, 0.5957, -0.0974, 0.3396, 0.2025, 0.6109, -0.4293, -0.0846], device='cuda:0', requires_grad=True) Parameter containing: tensor([[ 0.3228, 0.2529, 0.3183, -0.2758, 0.2793, -0.0019, -0.2335, 0.3072]], device='cuda:0', requires_grad=True) Parameter containing: tensor([0.0602], device='cuda:0', requires_grad=True)
该模型已经将张量注册为跟踪前向和反向传播所必须的特殊对象,在init初始化方法中定义nn神经网络层时会自动创建相应的张量并进行注册,也可以使用nn.parameter()函数手动注册这些参数。等价于如下代码:
1 2 3 4 5 6 7 8 9 10 11 class MyNeuralNet(nn.module): def __init__(self): super().__init__() self.input_to_hidden_layer = nn.parameter(torch.rand(2,8)) self.hidden_layer_activation = nn.ReLU() self.hidden_to_output_layer = nn.parameter(torch.rand(8,1)) def forward(self,x): x = x @ self.input_to_hidden_layer x = self.hidden_layer_activation(x) x = x @ self.hidden_to_output_layer return x
6.定义损失函数,由于需要预测连续输出,因此使用均方误差作为损失函数
1 loss_func = nn.MSELoss()
通过将输入值传递给神经网络对象,然后计算给定输入的损失函数值
1 2 3 4 5 6 7 8 _Y = mynet(X) #根据给定输入通过神经网络计算输出值 loss_value = loss_func(_Y,Y) #计算MSELoss值,注意在计算损失时,我们总是先传入预测结果,然后传入实际标记值 print(loss_value) #tensor(33.2581, device='cuda:0', grad_fn=<MseLossBackward0>)
7.定义降低损失值的优化器,优化器的输入是与神经网络相对应的参数(权重和偏差)以及更新权重时的学习率。本节我们使用随机梯度下降(SGD)。
1 2 from torch.optim import SGD opt = SGD(mynet.parameters(),lr = 0.001)
8.训练
训练神经网络的标准套路,每个epoch都会清空梯度 → 前向传播算预测 → 算 loss → 反向传播算梯度 → 用优化器更新参数 。
1 2 3 4 5 6 7 8 9 10 11 12 #一个epoch opt.zero_grad() #清除掉上一次训练时累积的梯度值,PyTorch 默认梯度是累加的(因为有时候需要多次backward() 再合并更新),所以每一轮训练之前都要把梯度清零,否则梯度会“越积越多”,参数更新就会出问题。 loss_value = loss_func(mynet(X),Y) #先用 mynet(X) 把输入数据跑一遍,得到预测值。然后拿预测值和真实标签 Y 做对比,算出误差(loss)。 loss_value.backward() #自动求导,计算每个参数的梯度 opt.step() #用刚才算好的梯度去更新参数。更新方式取决于优化器(比如 SGD, Adam),它会按公式调整权重,让 loss 变小。
1 2 3 4 5 6 7 8 #使用for循环重复执行上述步骤,执行50个epoch,此外loss_history列表存储每个epoch中的损失值。 loss_history = [] for _ in range(50): opt.zero_grad() loss_value = loss_func(mynet(X),Y) loss_value.backward() opt.step() loss_history.append(loss_value.item())
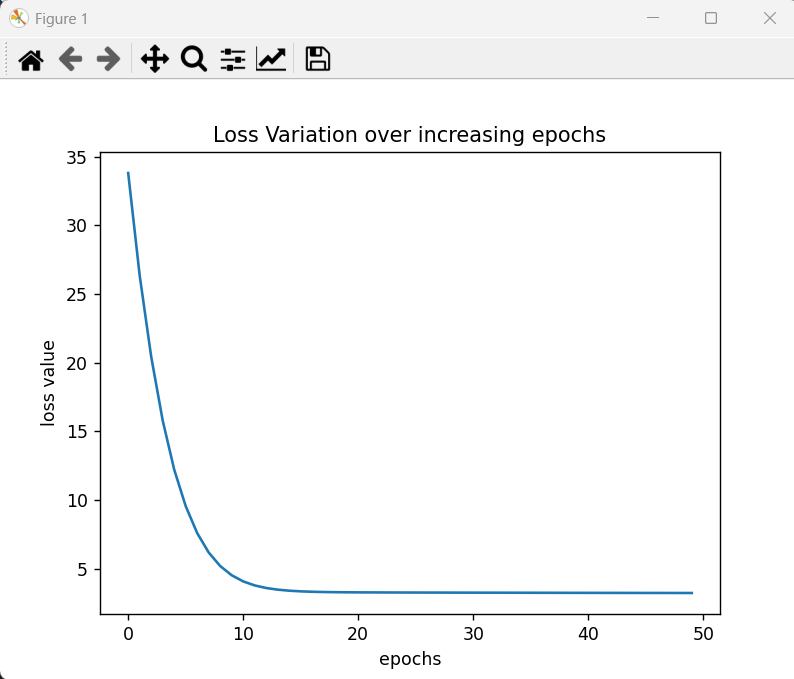
9.绘制损失随epoch的变化情况
1 2 3 4 5 6 import matplotlib.pyplot as plt plt.plot(loss_history) plt.title('Loss Variation over increasing epochs') plt.xlabel('epochs') plt.ylabel('loss value') plt.show()
2.神经网络数据加载 批大小(batch size)是神经网络中重要的超参数,批大小是指计算损失值或更新权重时考虑的数据样本数。假设数据集中有数百万个数据样本,一次将所有数据点用于一次权重更新并非最佳选择,因为内存可能无法容纳如此多数据。
1.导入加载数据和处理数据集的方法,导入数据将数据转换为浮点数,并将他们注册到相应设备中。
1 2 3 4 5 6 7 8 9 10 11 12 from torch.utils.data import Dataset,DataLoader import torch import torch.nn as nn x = [[1,2],[3,4],[5,6],[7,8]] y = [[3],[7],[11],[15]] X = torch.tensor(x).float() Y = torch.tensor(y).float() device = 'cuda' if torch.cuda.is_available() else 'cpu' X = X.to(device) Y = Y.to(device)
2.创建数据集类MyDataset:
Dataset的三个方法:init (self,x,y),len (self)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class MyDataset(Dataset): #存储数据信息以便可以将一批(batch)数据点捆绑在一起(使用DataLoader),并通过一次前向和反向传播更新权重。 #接受输入和输出 def __init__(self,x,y): self.x = x.clone().detach() #避免梯度信息污染数据集 self.y = y.clone().detach() #指定输入数据集的长度(__len__),(样本数) def __len__(self): return len(self.x) #getitem方法用于获取指定数据样本 def __getitem__(self,ix): return self.x[ix],self.y[ix] #ix表示要从数据集获取的数据索引,(输入+标签)
3.创建自定义类的实例
4.通过DataLoader传递数据集实例
1 dl = DataLoader(ds,batch_size=2,shuffle=True)
指定从ds输入数据集中获取两个(batch_size=2)的随机样本(shuffle=True)数据点。
1 2 3 4 5 6 7 8 9 for x,y in dl: print(x,y) #输出 #tensor([[5., 6.], [1., 2.]], device='cuda:0') tensor([[5.], [3.]], device='cuda:0') tensor([[3., 4.], [7., 8.]], device='cuda:0') tensor([[ 7.], [11.]], device='cuda:0')
生成两组输入-输出,因为原始数据集中共有4个数据点,而指定的批大小为2
5.定义神经网络类
1 2 3 4 5 6 7 8 9 10 11 class MyNeuralNet(nn.Module): def __init__(self): super().__init__() self.input_to_hidden_layer = nn.Linear(2,8) self.hidden_layer_activation = nn.ReLU() self.hidden_to_output_layer = nn.Linear(8,1) def forward(self,x): x = self.input_to_hidden_layer(x) x = self.hidden_layer_activation(x) x = self.hidden_to_output_layer(x) return x
6.定义模型对象(mynet),损失函数(loss_func)和优化器(opt):
1 2 3 4 5 mynet = MyNeuralNet().to(device) loss_func = nn.MSELoss() from torch.optim import SGD opt = SGD(mynet.parameters(),lr = 0.001)
7.循环遍历批数据点以最小化损失值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import time loss_history = [] start = time.time() for _ in range(50): for data in dl: x,y = data opt.zero_grad() loss_value = loss_func(mynet(x),y) loss_value.backward() opt.step() loss_history.append(loss_value.item()) end = time.time() print(end-start) #0.31676459312438965
与上一节相比,每个epoch更新权重的次数是原来的2倍,因为本节中使用的批大小是2,而上一节批大小为4,即以此使用全部数据点。
2.1模型测试 前面是如何在已知数据点上拟合数据,接下来介绍如何利用前面训练好的mynet模型中定义的前向传播方法来预测模型没有见过的数据点(测试数据)。
1.创建用于测试模型的数据点,并且将新数据点转换为张量浮点对象并注册到device中。
1 2 val_x = [[10,11]] val_x = torch.tensor(val_x).float().to(device)
2.通过训练好的神经网络(mynet)传递张量对象,与通过模型执行前向传播的方法相同:
1 2 print(mynet(val_x)) #tensor([[20.9521]], device='cuda:0', grad_fn=<AddmmBackward0>)
2.2获取中间层的值 在实际应用中,可能需要获取神经网络的中间层值,例如风格迁移和迁移学习等。pytorch提供了两种方式。
1.直接调用神经网络层,当成函数使用
1 print(mynet.hidden_layer_activation(mynet.input_to_hidden_layer(X)))
注意:必须按照模型输入、输出顺序调用相应神经网络层。input_to_hidden_layer的输出是hidden_layer_activation的输入。
2.forward方法指明想要查看的网络层
1 2 3 4 5 6 7 8 9 10 11 class MyNeuralNet(nn.Module): def __init__(self): super().__init__() self.input_to_hidden_layer = nn.Linear(2,8) self.hidden_layer_activation = nn.ReLU() self.hidden_to_output_layer = nn.Linear(8,1) def forward(self,x): hidden1 = self.input_to_hidden_layer(x) hidden2 = self.hidden_layer_activation(hidden1) x = self.hidden_to_output_layer(hidden2) return x,hidden2
通过以下代码访问隐藏层值,mynet的第0个索引输出的是网络前向传播的最终输出,而第一个索引输出的是隐藏层激活后的值。
3.使用Sequential类构建神经网络 除非需要构建一个复杂的网络,否则只需要利用Sequential类并指定层与层堆叠的顺序即可搭建神经网络。本节继续使用简单数据集训练神经网络。
1.导入相关的库,定义使用的设备,定义数据集与数据集类(MyDataset)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import torch import torch.nn as nn import numpy as np from torch.utils.data import Dataset,DataLoader device = 'cuda' if torch.cuda.is_available() else 'cpu' x = [[1,2],[3,4],[5,6],[7,8]] y = [[3],[7],[11],[15]] class MyDataset(Dataset): def __init__(self,x,y): self.x = torch.tensor(x).float().to(device) self.y = torch.tensor(y).float().to(device) def __len__(self): return len(self.x) def __getitem__(self,ix): return self.x[ix],self.y[ix]
2.定义数据集ds和数据加载对象dl
1 2 ds = MyDataset(x,y) dl = DataLoader(ds,batch_size = 2,shuffle = True)
3.使用nn模块中的Sequential类定义模型架构:
nn,Linear接受二维输入并为每个数据点提供八维输出,nn.ReLU在八维输出之上执行ReLU激活。最后使用nn.Linear接受八维输入并得到一维输出。
1 2 3 4 5 model = nn.Sequential( nn.Linear(2,8), nn.ReLU(), nn.Linear(8,1) ).to(device)
4.打印模型的摘要summary,查看模型架构信息
需要安装torchsummary库,pip install torchsummary
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 from torchsummary import summary print(summart(model,(2,)) #打印模型摘要,函数接受模型名称以及模型输入大小(需要使用整数元组)作为参数 #结果如下 ---------------------------------------------------------------- Layer (type) Output Shape Param # ================================================================ Linear-1 [-1, 8] 24 ReLU-2 [-1, 8] 0 Linear-3 [-1, 1] 9 ================================================================ Total params: 33 Trainable params: 33 Non-trainable params: 0 ---------------------------------------------------------------- Input size (MB): 0.00 Forward/backward pass size (MB): 0.00 Params size (MB): 0.00 Estimated Total Size (MB): 0.00 ---------------------------------------------------------------- None
以第一层输出为例,形状为(-1,8),其中-1表示batch size,8表示对于每个数据点都会得到一个8维输出,得到形状为batch size×8的输出。
5.接下来定义损失函数loss_func和优化器opt并训练模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 loss_func = nn.MSELoss() from torch.optim import SGD opt = SGD(model.parameters(),lr = 0.001) import time loss_history = [] start = time.time() for _ in range(50): for ix,iy in dl: opt.zero_grad() loss_value = loss_func(model(ix),iy) loss_value.backward() opt.step() loss_history.append(loss_value.item()) end = time.time() print(end-start) #0.18243002891540527
6.训练模型后,在验证数据集上预测值
定义预测数据集:
1 val = [[8,9],[10,11],[1.5,2.5]]
将验证数据转换为浮点数并转换为张量对象存储到device中,模型传递验证数据预测输出
1 2 3 4 5 6 7 val = torch.tensor(val).float() print(model(val.to(device))) #结果为 #tensor([[16.8575], [20.7629], [ 4.1649]], device='cuda:0', grad_fn=<AddmmBackward0>)
4.pytorch模型的保存与加载 神经网络处理的一个重要方面就是在训练后保存和加载模型,保存模型之后,我们可以利用已经训练好的模型进行推断,只需要加载已经训练好的模型,而无需再次对其进行训练。
4.1模型保存所需组件
4.2模型状态
1 2 3 4 5 6 7 8 9 10 11 12 13 print(model.state_dict()) """ OrderedDict([('0.weight', tensor([[ 0.8770, 0.1810], [-0.2726, -0.5457], [-0.3269, -0.5528], [ 0.5133, -0.3993], [ 0.6862, 0.6442], [ 0.1152, -0.6341], [ 0.3632, -0.3292], [-0.1101, 0.1117]], device='cuda:0')), ('0.bias', tensor([-0.0707, -0.0403, -0.1827, -0.5141, 0.2934, 0.6227, -0.3822, -0.3792], device='cuda:0')), ('2.weight', tensor([[ 0.6465, -0.2204, -0.2875, -0.1880, 0.9614, -0.1798, 0.0300, -0.2467]], device='cuda:0')), ('2.bias', tensor([0.2132], device='cuda:0'))]) """
4.3模型保存
1 2 save_path = 'mymodel.pth' torch.save(model.state_dict(),save_path)
4.4模型加载 加载模型首先需要初始化模型,然后从state_dict加载权重 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 import torch from torch import nn device = 'cuda' if torch.cuda.is_available() else 'cpu' model = nn.Sequential( nn.Linear(2,8), nn.ReLU(), nn.Linear(8,1) ).to(device) #使用与训练时相同的代码创建一个空模型 state_dict = torch.load('mymodel.pth') #从磁盘加载模型并反序列化以创建一个OrderedDict值 model.load_state_dict(state_dict) model.to(device) #加载state_dict到模型中,并将其注册到device中,执行预测任务 val = [[8,9],[10,11],[1.5,2.5]] val = torch.tensor(val).float() print(model(val.to(device))) #输出 #tensor([[16.7941], [20.6560], [ 4.2427]], device='cuda:0', grad_fn=<AddmmBackward0>)