深度学习第二节（神经网络与模型训练过程）

1.人工神经网络基础

​ ANN是张量（权重，weights）和数学运算的集合，将一个或者多个张量作为输入并预测相应输出。将输入连接到输出的操作方式称为神经网络的架构，我们可以根据不同的任务构建不同架构，即基于问题是包含结构化数据还是非结构化数据（图像、文本、语言）数据，这些数据就是输入和输出张量的列表。ANN由以下部分组成：

​ 输入层：将自变量作为输入

​ 隐藏层：连接输入和输出，在输入数据之上进行转换；此外，隐藏层利用节点单元将输入值修改为更高/更低维的值；通过修改中间节点的激活函数可以实现复杂表示函数。

​ 输出层：输入变量产生的值，取决于实际任务以及我们是在尝试预测连续变量还是分类变量。如果输出是连续变量，则输出有一个节点。如果输出是具有m个可能类别的分类，则输出有m个节点

典型结构为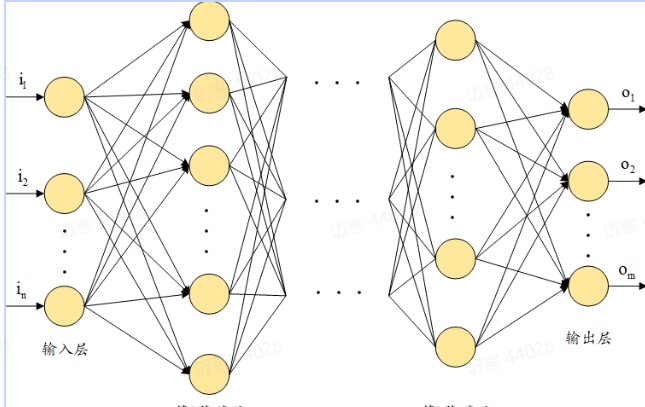：image-20250912201532438

1.1神经网络的训练

​ 训练神经网络实际上是通过重复两个关键步骤来调整神经网络中的权重：前向传播和反向传播。

1.在前向传播中，我们将一组权重应用与输入数据，将其传递给隐藏层，对隐藏层计算后的输出使用非线性激活，通过若干个隐藏层后，将最后一个隐藏层的输出与另一组权重相乘，就可以得到输出层的结果。对于第一次正向传播，权重的值将随机初始化。

2.反向传播中，尝试通过测量输出的误差，然后相应调整权重以降低误差。神经网络重复正向和反向传播以预测输出，直到获得令误差较小的权重为止。

1.2常用的激活函数

​ 激活函数有助于对输入和输出之间的复杂关系进行建模，使用他们可以实现高度非线性。常用的激活函数如下：

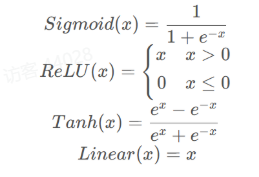
image-20250912202912683

​ 应用激活函数之后，输入值对应的激活可视化如下：

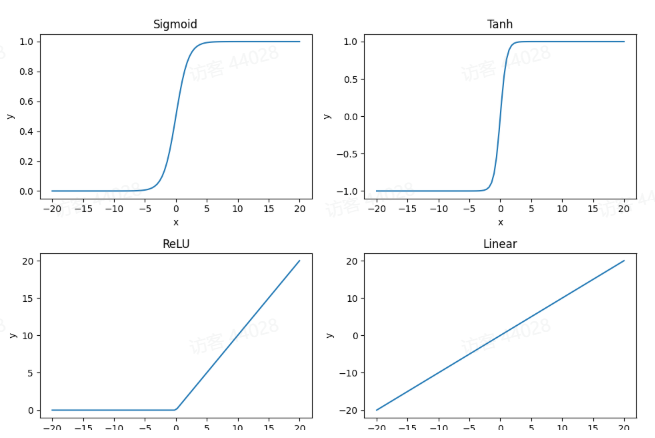
image-20250912202948739

1.3计算损失值

​ 损失值，也称之为成本函数，是我们需要在神经网络中优化的值。分为两种情况：分类（离散）变量预测和连续变量预测

1.3.1在连续变量预测过程中计算损失

​ 通常当变量为连续的时候，可以计算实际值和预测值之差的平方的平均值作为损失值，也就是改变与神经网络相关的权重值来最小化均方误差。

image-20250912203748085

1.3.2在分类（离散）变量预测计算过程中计算损失

​ 当要预测的变量是离散的时候，我们通常使用分类交叉熵损失函数，当要预测的变量有两个不同的值时，损失函数为二元交叉熵。二元交叉熵计算如下：

image-20250912204016629

2.实现前向传播

(本文中的使用numpy构建神经网络不是最佳方法）)

1.通过将输入值乘以权重来神经元输出值

2.计算激活值

3.在每个神经元上重复前两个步骤，直到输出层

4.将预测输出与真实值进行比较计算损失值

将以上过程封装成一个函数，将输入数据、当前神经网络权重和真是值作为函数输入，并返回网络的当前损失值。

1
2
3
4
5
6
7
import numpy as np
def feed_forward(inputs,outputs,weights):
	pre_hidden = np.dot(inputs,weights[0])+weights[1]
	hidden = 1/(1+np.exp(-pre_hidden))#sigmod激活函数
	pred_out = np.dot(hidden,weights[2])+weights[3]
	mean_squared_error = np.mean(np.square(pred_out-outputs))#均方误差
	return mean_squared_error

​ 由于为每个神经元节点添加偏置项，因此权重数组不仅包含连接不同节点的权重，还包含与隐藏层/输出层中的节点相关的偏置项

1
pre_hidden = np.dot(inputs,weights[0])+weights[1]

​ 通过执行输入层和权重层（weights[0])的矩阵乘法来计算隐藏层值，并将偏置（weights[1]）添加到隐藏层中，利用权重和偏置值就可以将输入层连接到隐藏层。

3.实现反向传播

​ 反向传播中利用前向传播中计算的损失值，尽可能最小化损失值为目标更新网络权重。步骤如下：

image-20250912215502325

​ 在整个数据集上执行n次上述过程（包括前向传播和反向传播），表示模型进行了n个epoch的训练（执行一次称为一个epoch）

​ 由于神经网络可能包含数以百万的权重，因此更改每个权重的值，并检查损失的变化在实践中并不是最佳方法。上述步骤的核心就是计算权重变化的损失变化，即计算损失值关于权重的梯度。

3.1梯度下降

​ 更新权重以减少误差值的整个过程称为梯度下降，随机梯度下降（SGD）是将误差最小化的一种方法，其中随机表示随机选择数据集中训练数据样本，并根据样本做出决策。除了随机梯度下降外，还有许多别的优化器。

1
2
3
4
5
6
7
8
9
#定义前馈网络并计算均方误差损失值
from copy import deepcopy
import numpy as np
def feed_forward(inputs,outputs,weights):
	pre_hidden = np.dot(inputs,weights[0])+weights[1]
	hidden = 1/(1+np.exp(-pre_hidden))#sigmod激活函数
	pred_out = np.dot(hidden,weights[2])+weights[3]
	mean_squared_error = np.mean(np.square(pred_out-outputs))#均方误差
	return mean_squared_error

1.为每一个权重和偏置项增加一个非常小的值（0.0001），并针对每个权重和偏差的更新计算一个平方误差损失值。（学习率lr）

1
def update_weights(inputs,outputs,weights,lr):

2.由于权重需要在后续步骤中进行操作，因此使用deepcopy确保我们可以处理多个权重副本，而不会影响实际权重，创建作为输入传递给函数的原始权重集的三个副本——original_weights,temp_weights,updated_weights:

1
2
3
original_weights = deepcopy(weights)
temp_weights = deepcopy(weights)
updated_weights = deepcopy(weights)

3.使用原始权重集计算损失值

1
original_loss = feed_forward(inputs,outputs,weights)

4.遍历网络的所有层

1
2
3
4
5
6
7
8
9
10
	for i,layer in enumerate(original_weights):
		for index,weight in np.ndenumerate(layer):
		#示例神经网络中包含四个参数列表，前两个列表分别表示将输入连接到隐藏#层的权重和偏置项参数，另外两个表示连接隐藏层和输出层的权重和偏置参数。#np.ndenumerate循环遍历给定列表中的每个参数
		temp_weights = deepcopy(weights)
		temp_weights[i][index] += 0.0001
		_loss_plus = feed_forward(inputs,outputs,temp_weights)
#将temp_weights重置为原始权重集，因为在每次迭代中，都需要更新一个参数以计算#对参数进行小量更新时的损失。
		grad = (_loss_plus - original_loss)/(0.0001)#计算由于权重变化##引起的梯度（损失值的变化）
		update_weights[i][index] -= grad*lr #使用学习率lr令权重变化更加#稳定
	return updated_weights,original_loss

​ 在实践中，我们通常会一次使用一批数据应用梯度下降更新网络参数，直到再一次训练周期（epoch）内遍历所有数据点。构建模型时，批大小通常为32到1024之间。

3.2使用链式法则实现反向传播

​ 当网络参数较多时，梯度下降法更新权重值需要进行大量计算来得到损失值，需要大量资源和时间。接下来介绍如何利用链式法则来获取与权重值有关的损失梯度。

image-20250912215200977 image-20250912215420281 image-20250912215034916

3.合并前向传播和反向传播

​ 实现一个简单的数据集，模型定义如下：输入连接到具有三个神经元（节点）的隐藏层，隐藏层连接到具有一个神经元的输出层。

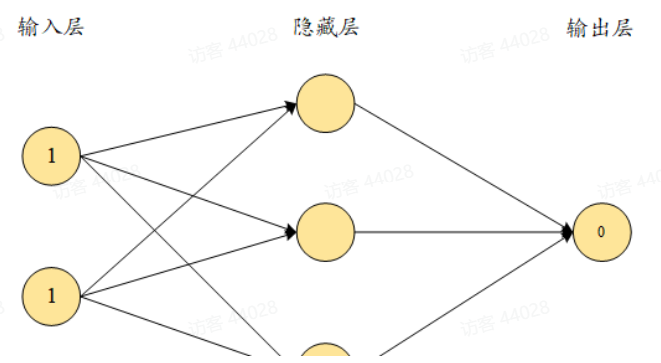
image-20250913095029576

1.导入相关的库并定义数据集

1
2
3
4
5
import numpy as np
from copy import deepcopy
import matplotlib.pyplot as plt
x = np.array([[1,1]])
y = np.array([[0]])

2.随机初始化权重和偏置

​ 由于隐藏层中有三个神经元，每个输入节点都连接到隐藏层单元。因此共有六个权重值和三个偏置值，也就是说每个隐藏层神经元包含一个偏置和两个权重（每个输入到隐藏层神经元的连接都对应一个权重）；最后一层有一个神经元连接到隐藏层的三个d单 元，因此包含三个权重和一个偏置值。随机初始化：

1
2
3
4
5
6
7
8
W = [
	np.array([[-0.0052,0.3793],
			[-0.5820,-0.5204],
			[-0.2723,0.1896]],dtype = np.float32).T,
	np.array([-0.0140,0.5607,-0.1135],dtype = np.float32).T,
	np.array([[0.1528,-0.1745,-0.1135]],dtype = np.float32).T,
	np.array([-0.5516],dtype = np.float32)
]

3.在100个epoch内执行前向传播和反向传播，使用以上部分定义的feed_forward和update_weights函数。训练期间，更新权重并获取损失值和更新后的权重值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def feed_forward(inputs,outputs,weights):
	pre_hidden = np.dot(inputs,weights[0])+weights[1]
	hidden = 1/(1+np.exp(-pre_hidden))
	out = np.dot(hidden,weights[2])+weights[3]
	mean_squared_error = np.mean(np.square(out-outputs))#MSE均方误差
	return mean_squared_error
	
def update_weights(inputs,outputs,weights,lr):
	original_weights = deepcopy(weights)
	#temp_weights = deepcopy(weights)
	updated_weights = deepcopy(weights)
	original_loss = feed_forward(inputs,outputs,original_weights)
	for i ,layer in enumerate(original_weights):
		for index,weights in np.ndenumerate(layer):
			temp_weights = deepcopy(original_weights)
			temp_weights[i][index] += 0.0001
			_loss_plus = feed_forward(inputs,outputs,temp_weights)
			grad = (_loss_plus - original_loss)/(0.0001)
			updated_weights[i][index] -= grad*lr	
	return updated_weights,original_loss

4.绘制损失值

1
2
3
4
5
6
7
8
9
losses = []
for epoch in range(100):
	W,loss = update_weights(x,y,W,0.01)
	losses.append(loss)
plt.plot(losses)
plt.title('Loss over increasing number of epochs')
plt.xlabel('Epochs')
plt.ylabel('Loss value')
plt.show()

5.获取更新的权重后，通过将输入传递给网络进行预测并计算输出值

1
2
3
4
5
print(W)
pre_hidden = np.dot(x,W[0]) + W[1]
hidden = 1/(1+np.exp(-pre_hidden))
pred_out = np.dot(hidden,W[2]) + W[3]
print(pred_out)

4.神经网络训练过程总结

​ 训练神经网络主要通过两个关键步骤，即以给定的学习率进行前向传播和反向传播，最终神经网络架构得到最佳权重。需要注意的是第一次前向传播时，权重的值是随机初始化的。在反向传播中，通过在损失减少的方向上调整权重来减少损失值（误差），权重更新的幅度等于梯度乘以学习率。重复前向传播和反向传播的过程，知道获得尽可能小的损失，在训练结束时，神经网络已经将权重调整到近似最优值，以便获取期望的输出结果。